c program to draw 3d cube
3D graphics is what games are all about today. At the fourth dimension the Commodore 64 and other eight bit computers were common, 2D games were the virtually popular. Notwithstanding, some 3D titles were available for these machines, and they represented technical marvels at the time. I think Freescape games (similar Driller or Castle Main) were the most advanced 3D software bachelor back then. The Sinclair Spectrum could offer very good speed performances with such games, while the Commodore 64 was somewhat slower. Just, it could offer better colors and in-game music. Equally mathematics is all that is backside 3D vector graphics, the Z80 commonly enjoys an reward over the 6510 as information technology is slightly faster and information technology has 16 scrap internal registers. The Commodore 64 can practice the calculations required every bit well, just due to the pure 8 bit nature of the 6510 and its clock speed, calculations will accept more time. Comport in mind however that Z80 instructions ordinarily crave more cycles than 6510 ones, so the Z80 is not every bit faster as the clock speed ratio may lead you remember. Nonetheless, efficient programming allows for dainty 3D performances on the Commodore 64 as well, and games similar "Stunt Car Racer" are an evidence of this.


Only what's inside 3D graphics? First of all, nosotros are talking about true 3D graphics here, that is, 3D graphics based on vector calculations. 3D furnishings may be accomplished even without using vectors actually, merely such routines are not true 3D (this is an example).
What is a vector? On a 2d plane (that is, a drawing canvass or the screen) each indicate may be represented mathematically past using a vector. A coordinate system can be used, and then that y'all tin can tell the position of each point.
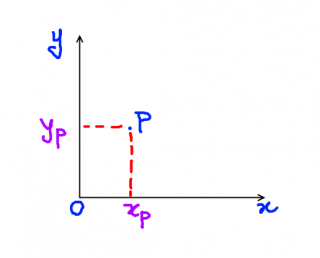
2 axes (ten and y) are used (they are positive in the management of the arrows). The point P tin can exist plant on the plane by using the coordinates xp (10 coordinate) and yp (y coordinate). The betoken can be expressed every bit P (xp, yp). This is called a vector, every bit information technology is not a simple number but a couple of numbers (this is NOT the true definition of a vector actually, simply that'south but what can be enough here).
On 3D space, three axes are necessary. That means, a signal on infinite can be plant by using three coordinates (x, y and z coordinate). On 2D you have width and height – 3D adds dept.
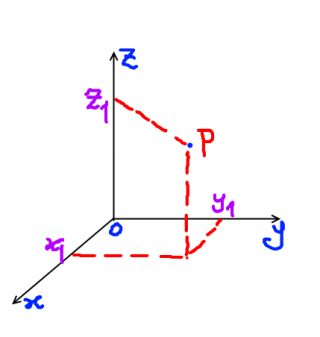
So, a bespeak on space can be represented past the vector P(x1, y1, z1).Only imagine a vector equally a gear up of given coordinates that make up a signal.
A wireframe 3D cube is a cube whose vertexes are represented by vector points, joined together by lines. That's exactly what we volition be cartoon. So, nosotros just have to detect the coordinates of each vertex, like on the previous picture.
If we center the cube to the origin O, the coordinates of the eye of the cube are of class (0, 0, 0) and if the size of the cube is 2*Fifty, it's easy to see that its vertexes tin can be represented by the post-obit vectors:
p1 = (-Fifty, -L, -Fifty) p2 = (-L, 50, -L) p3 = (Fifty, L, -L) p4 = (Fifty, -Fifty, -Fifty) p5 = (-L, -L, Fifty) p6 = (-Fifty, L, L) p7 = (L, L, Fifty) p8 = (L, -L, L)
Now, the trouble is drawing the cube. As the screen is a 2D airplane, how dept can be represented?
Nosotros need a formula to project the points that is capable of keeping dept into business relationship. That fashion, we will make the illusion of a solid object, fifty-fifty if it is drawn on the plane.
Vertex coordinates on the screen (two coordinates) can be calculated as follows:
vx = 160 + (10*fs)/(z + fs) vy = 100 + (y*fs)/(z + fs)
vx and vy are just the x and y coordinates of the point to plot on the screen.
fs is a scale gene that determines how much the cube is zoomed. In the code that will follow a value of 200 has been used. As you can see, 10 and y coordinates are transformed using the dept z. That is what is giving the illusion of dept that nosotros need.
The numbers 160 and 100 are dealing with the resolution of the screen. As the Commodore 64 screen is 320 x 200, the theoretical origin (0,0) used earlier actually becomes (160,100). And all points are merely translated like that. We will use the 320 ten 200 resolution even on the PC, just to accept an idea of what the C64 version may look like.
Once nosotros have drawn the cube, we can rotate it. Rotation of a solid tin can exist performed about the x, y or z axes. Rotations can be combined and then that a more sophisticated move can be accomplished.
The idea is to employ mathematical relations that will change the coordinates of a indicate according to the rotation bending. If we want to rotate the cube nearly the z axes, only x and y coordinates must be inverse. If we want to rotate the cube almost the x axes, just the y and z coordinates must be changed, then on. Those transformations can exist expressed as linear combinations of the coordinates of the point to be rotated and of the sine and cosine functions evaluated on the rotation angle.
Without any farther explanation, hither is the Freebasic (PC) lawmaking:
3D rotating cube (Freebasic sourcecode)
The cube is drawn by plotting lines between its vertexes. Notice that the code hither is quite simple and it does non perform hidden lines clipping. So, the shape of the cube may be a footling confusing at times, but its geometry is actually correct.
A simple Simons' Bones version that tin can be run on the Commodore 64 is as follows:
Simons' Basic 3D cube
Simons' BASIC tin be downloaded hither.

The Simons' BASIC version is obviously quite tedious, but information technology demonstrates the concept. If you employ a C64 emulator (for instance, X64 on VICE), information technology is possible to prepare emulation speed to 1500% so that the animation can be performed at a decent speed.
Auto language is the key to get such a program running fast on the Commodore 64, that'southward clear. We already have the instruments needed to lawmaking such a programme, as we take already coded programs that tin draw lines, perform multiplications and divisions (please check that aforementioned line drawing programme and this article), evaluate sine and cosine functions. We just take to put things together. But, those programs are not optimized in order to become skillful performances on 3D. The approach used on the lines drawing program has been useful to test my integer math routines, but it was not aimed at speed. So, simpler and faster line drawing routines must be developed.
A Commodore 64 assembly implementation can be found on this article.
Source: https://retro64.altervista.org/blog/3d-graphics-rotating-cube-with-freebasic-pc-and-simons-basic-c64/
Postar um comentário for "c program to draw 3d cube"